Различные трактовки термина бифуркации
Особое значение (в синергетике) имеет момент выбора между различными аттракторами, развилка дорог эволюции. Для обозначения этого решающего момента используется термин бифуркация. Путь эволюции становится жестко предзадан только после попадания в воронку аттрактора и прохождения точки бифуркации. На сцену выходит фактор случайности.
Жизненный путь каждого человека содержит множество моментов решающего выбора, цепь бифуркаций. По сути дела, синергетическую картину жизни рисует В. В. Набоков: "Есть острая забава в том, чтобы, оглядываясь на прошлое, спрашивать себя, что было бы, если бы... заменять одну случайность другой, наблюдать, как из какой-нибудь серой минуты жизни, прошедшей незаметно и бесплодно, вырастает дивное розовое событие, которое в свое время так и не вылупилось, не просияло. Таинственная эта ветвистость жизни, в каждом былом мгновении чувствуется распутие, - было так, а могло бы быть иначе, - и тянутся, двоятся, троятся несметные огненные извилины по темному полю прошлого".
Чем более неустойчива система, чем ближе она к моменту обострения или к точке бифуркации, тем более чувствительной она делается ко всей массе влияний, вносимых как с нижележащих, так и вышележащих уровней бытия.
Бифуркации
Под влиянием поступающих в систему ресурсов (вещество, энергия, информация) и складывающихся внешних условий в ней медленно накапливаются количественные изменения, ситуация постепенно обостряется: между ее отдельными элементами рвутся старые связи и возникают новые, разрушаются некоторые старые элементы и зарождаются новые. Происходящие изменения иногда бывают столь масштабны и значительны, что система может оказаться в неустойчивом состоянии. Этот поворотный момент в ее жизни называют точкой бифуркации (от лат. bifurcus - раздвоенный, вилка).
Это состояние, хотя и неустойчиво, но имеет перспективу в плане обновления системы, это точка "выбора" дальнейшего пути развития. Его определяет соотношение между двумя противоположными тенденциями. С одной стороны, ресурсные потоки и случайные флуктуации провоцируют повышение энтропии системы, что ведет к нарастанию хаоса и, в конечном итоге, может привести к ее разрушению. С другой - система стремится сохранить устойчивость за счет переструктурирования и формирования нового порядка, и таким образом снизить энтропию. Какая из них будет преобладать, зависит от множества случайных факторов и во многом определяется внешними и внутренними условиями, а также качеством поступающих ресурсов.
Фракталы

В точках бифуркации перед самоорганизующейся системой открывается множество вариантов (поле) путей развития. Одновременно возникает множество диссипативных динамических микроструктур - праобразов будущих состояний системы - фракталов (англ. fractial - дробный).
В окружающей нас природе мы можем встретить множество таких образований: лапы ели, перо птицы, рисунок на крыле бабочки. Человек давно подметил эту красоту и старался воспроизвести ее в симметрии различных орнаментов.
В точке бифуркации происходит своеобразная конкуренция фракталов, осуществляется их "отбор", идет "борьба за выживание" в новых условиях. В результате конкуренции происходит самопроизвольный выбор той структуры, которая наиболее адаптивна к сложившимся на данный момент внешним и внутренним условиям.
Большинство из фракталов нежизнеспособны, так как оказываются невыгодными с точки зрения фундаментальных законов природы (законы сохранения массы-энергии, энтропии-информации, принцип минимизации энергии и др.). Они либо разрушаются полностью, либо остаются как отдельные рудименты, архаические остатки прошлого, с которыми мы нередко сталкиваемся не только в мире природы, но и в жизни общества, языке и культуре народов.
Аттракторы
Но даже, если система развивается сообразно этим законам, картина ее будущего весьма неопределенна и принципиально непредсказуема в силу фундаментальной роли случайного. Именно случайность выступает изобретателем и творцом будущего. Случайное слабое внешнее воздействие или слабые флуктуации внутренних параметров, "приуроченные" к определенному моменту развития системы, могут привести к большим ее внутренним изменениям. Флуктуации возникают хаотично, их огромное количество, но большинство из них затухает, как бы отсекаются все лишние вихревые потоки, остаются только те, которые образуют новые устойчивые макросостояния (структуры) - аттракторы. Аттрактор как бы притягивает к себе множество траекторий развития системы, определяемых разными начальными значениями параметров, создавая своеобразный конус. В качестве его наглядной модели можно использовать рисунок на раковинах некоторых моллюсков.

Если неустойчивая микроструктура попадает в конус аттрактора, то она неизбежно эволюционирует к устойчивому состоянию и может находиться в нем до тех пор, пока в силу каких-либо причин система вновь не придет в неустойчивое состояние. Эти причины связаны с несоответствием внутреннего состояния открытой системы внешним условиям среды. И опять у системы возникает множество вариантов развития. Эта направленная череда событий, этот бесконечный круговорот созиданий и разрушений, с которым связано обновление, усложнение и совершенствование системы есть ни что иное, как эволюция.
Наглядно этот процесс можно представить в виде эволюционного дерева биологических видов или антропогенеза. Это аналоги диаграммы бифуркаций в синергетике.
Эволюционное древо системы
Поведение системы в точке бифуркации подобно блужданию по лабиринту со множеством тупиков. "Выбор" пути развития осуществляется методом проб и ошибок до тех пор, пока она не "находит" оптимальный вариант. Здесь чрезвычайно важную роль играют кооперативные (совместные) процессы, основывающиеся на когерентном (согласованном) взаимодействии элементов зарождающейся фрактальной структуры. Это взаимоподдерживающее соразвитие элементов, способствующее сохранению устойчивости развития системы, получило название коэволюции.
При благоприятных условиях какой-то из фракталов "разрастается" и перерождается в новую макроструктуру. В результате этого система переходит в новое качественное состояние. "Выбрав" его, она продолжает поступательное движение до следующей точки бифуркации. Этот самопроизвольный процесс усложнения и совершенствования системы периодически повторяется и может продолжаться бесконечно долго. Но всегда есть внешние факторы (потоки информации, энергии, вещества), которые как бы подталкивают систему к самоорганизации. Например, самоорганизация биосферы осуществляется благодаря энергии Солнца, работа лазера - благодаря энергии накачки и т.д.
Не по такому ли сценарию происходит эволюция всех природных систем?
БИФУРКАЦИИ В МОДЕЛЯХ ПОПУЛЯЦИЙ
Чудо фрактальной геометрии заключается в том, что чрезвычайно сложные формы могут получаться из таких простых процессов генерирования. Еще один сюрприз преподносит нам учение о динамических системах: такие простые, детерминированные уравнения могут порождать такое хаотическое поведение, при котором система никогда не возвращается в стабильное состояние и не проявляется никакой закономерности. Часто такие системы ведут себя вполне нормально до некоторого определенного значения ключевого параметра, потом испытывают переход и в котором существует две возможности дальнейшего развития, потом четыре, и, наконец, хаотический набор возможностей.
В 1786 году Томас Мальтус разработал математическую модель роста популяций и оказалось, что эта и другие модели подобного типа обладают описанным выше свойством. Предположим, что у нас есть модель в которой скорость роста популяции это функция, в частности, от численности популяции:
Новая популяция = скорость роста * старая популяция (1 - старая популяция)
Где популяция нормализована так, что она принимает значения от 0 до 1. Естественно, такая модель является сильно упрощенной и не может достаточно точно описывать динамику развития популяций. При скорости роста меньше 200%, эта модель стабильна, т.к. для любого начального значения, после нескольких поколений, численность популяции устанавливается на стабильном уровне. Но если скорость роста превышает 200%, кривая, графически отображающая уравнение, разделяется или бифурцирует на два дискретных решения, затем на четыре, и вскоре становится хаотической.
ДЕРЕВО ФЕЙГЕНБАУМА
Логистическое уравнение - это формула, над которой, в основном, работал Митчел Фейгенбаум при создании своей теории о фракталах. Эта формула должна описывать динамику развития популяции:
f(x) = (1 - x)rx
Простейшая модель - это пропорциональное соотношение численности с прошлым годом. Допустим в прошлом году у нас было x животных. В этом году их должно быть rx животных. Но это не выполняется в реальных условиях. Лучшее соответствие с реальностью получится если добавить фактор, зависящий от того какой потенциал существует у популяции для дальнейшего развития, и пусть x - коэффициент полноты, который меняется от 0 до 1. Потом добавляется фактор 1 - x, так что территория почти полностью заполнена, популяция не возрастет выше верхнего предела.
Расширяя логистическое выражение, получаем:
f(x) = аx - ах2
Формула, использующаяся в программе LT Bifurcator для объяснения сущности фрактала Фейгенбаума - (1 + r)x - rx2 не сильно отличается от формулы, приведенной выше. В принципе, для изучения теории можно было использовать любую формулу, например самую простую из формул данного вида - xІ - r. Единственными различиями являются различия в координатах окон на картинке и несколько измененный внешний вид изображения. 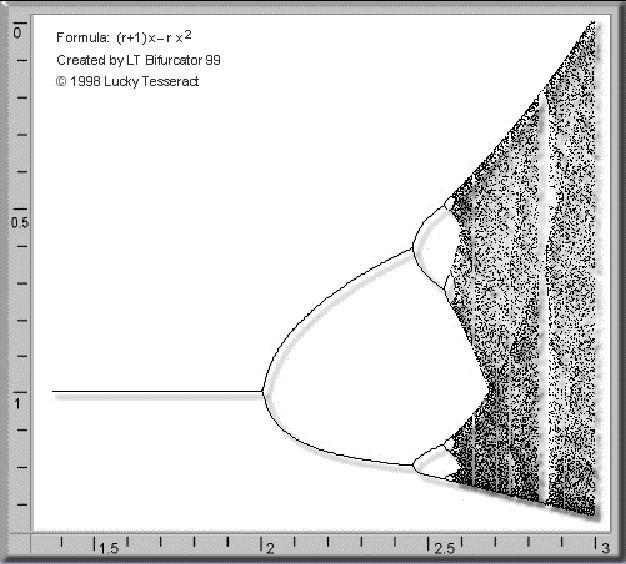
БИФУРКАЦИИ И САМООРГАНИЗАЦИЯ
I. Эволюция и сложность
Взглянув на окружающий нас мир, мы обнаружим неисчерпаемое разнообразие вещей и явлений: солнце, ветер, дождь и многочисленные сложные погодные процессы, изобилующий формами и красками мир растений, рыб в коралловых рифах, царство животных и окружающий нас рукотворный мир человека. Ночью мы наблюдаем звездное небо и получаем возможность заглянуть в процессы, разыгрывающиес на больших пространственных и временных расстояниях от нас. Все это есть проявление сложности и все это - в движении, все развивается, эволиционизирует
II. Самоорганизация
Опыт повседневной жизни и целенаправленное наблюдение процессов в природе и общественных явлений учат нас, что многие сложные системы, состоящие из большого числа взаимодействующих подсистем, при определенных условиях обладают способностью к самоорганизации и эволюции. Самым замечательным тому примером могут служить живые существа и их развитие на нашей планете (от сине-зеленых водорослей до человека с его интеллектом), самоорганизаци толпы, аплодирующие зрители, установление цен на рынке.
Под самоорганизацией понимается необратимый процесс (обратный процесс невозможен или крайне мало вероятен), приводящий в результате кооперативного (совместного) действия подсистем к образованию более сложных структур всей системы. Самоорганизаци - элементарный процесс эволюции, состоящей в неограниченной последовательности процессов самоорганизации.
Основное, что отличает самоорганизацию от других процессов, например, от процессов роста, является качественное изменение состояния, в котором находится система, и это изменение происходит скачком.
III. О фазах и процессах эволюции
История эволюции есть история возникновени все более сложных структур из более простых, ведь суть эволюции состоит как раз в интеграции (объединении) более простых элементов в целостные образования более высокого уровня, т. е. в более сложные системы, характеризуемые новыми качествами.
Наиболее важными фазами эволюции окружающего нас мира были следующие:
космическая эволюция (Большой взрыв, образование элементарных частиц, формирование атомов и молекул, возникновение галактик, звезд и планет, образование "фотонной мельницы");
химическая эволюция (образование системы химических элементов и соединений, возникновение органических соединений, полимеризаци в цепи органических молекул);
геологическая эволюция (образование структур земной коры, гор, вод и т.д.);
эволюция протоклетки (самоорганизация полимеров и хранение информации на молекулярном уровне, пространственная индивидуализация, возникновение молекулярного языка);
дарвиновская эволюция (развитие видов животных и растений, и их взаимодействие, возникновение экосистемы на земле);
Примечание: Дарвин создал и обосновал теорию происхождени видов, сформулировал принцип отбора и продемонстрировал его значение для эволюции в биологии (1838 г.)
эволюция человека (развитие труда, языка и мышления);
Примечание: Шлейхер установил аналогичный дарвиновскому принцип для развития естественных языков (1850 г.) и тем самым заложил основы теории языковой коммуникации.
эволюция общества (развитие распределения труда, общественна организация, техника, общественные формации и т.д.);
эволюция информации и обмена информации (обогащение и хранение знания, развитие связи, науки и т.д.).
IV. Об общей структуре процессов эволюции
Итак, эволюцию можно рассматривать как неограниченную последовательность процессов самоорганизации.

Относительно стабильное N-ое состояние эволюции системы утрачивает устойчивость. В качестве причин, вызывающих потерю устойчивости, выступают временные изменения внутреннего состояния (например, старение) или внешние условия (например, изменение температуры среды, в которой находится заполненная водой и закупоренная бутылка).
Особенно характерной причиной эволюционной неустойчивости является внезапное появление новой моды (вида, формы) движения, новой разновидности молекул в химии, нового вида в биологии. Этот новый элемент в рассматриваемой динамической системе приводит к потере устойчивости состояния системы, которое до появления нового элемента было устойчивым.
1. Неустойчивость, обусловленная новым элементом в системе, запускает динамический процесс, который приводит к дальнейшей самоорганизации системы. Система порождает новые упорядоченные структуры.
2. По завершению процесса самоорганизации эволюционизирующая система переходит в состояние (n+1). После этого n-го эволюционного цикла начинается новый (n+1)-й цикл.
В конечном результате циклов самоорганизации заключены как малые, так и большие скачки эволюции. Характерно, что реальна эволюция никогда не заканчивается, она каким-то образом находит выход (неустойчивость) из любого тупика и этот выход приводит к новому циклу самоорганизации. Поскольку каждый парциальный (единичный, отдельный) процесс поднимает систему на новую , в определенном смысле более высокую плоскость, весь процесс в целом обладает спиральной структурой.
В качестве примера рассмотрим биологические виды, занимающие на определенной территории одну экологическую нишу. При внедрении нового вида, который существенно лучше использует ту же нишу, наступает фаза перехода от сосуществования к полному вытеснению исходных видов. При этом такие переходы повышают селекционную ценность смешанной популяции от ценности старой популяции до ценности новой.
V. Бифуркации
Выдержка из книги "Синергетика и прогнозы будущего" (авторы С.П.Капица, С.П.Курдюмов, Г.Г.Малинецкий): "Одна из ключевых идей нелинейной науки (изучающей поведение нелинейных систем), выдвинутая в начале XX века Анри Пуанкаре, выдающимся французским математиком, по существу, пришла из истории". Что делает гуманитарий, когда хочет понять какое-то явление в истории? Он смотрит, что этим событиям предшествовало и к чему они привели. Он интересуется, что было аналогичного в других странах в другие эпохи. При этом особое внимание уделяется переломным эпохам и возникновению новых качеств. Это называется "историческим подходом". Но именно так сейчас поступают в одном из разделов нелинейной науки - теории ветвления или бифуркаций (от французского la bifurkation).
Суть бифуркации лучше всего иллюстрирует витязь на распутье, который стоит перед камнем с надписью "Направо пойти - женатому быть, налево пойти - коня потерять, прямо пойти - буйную. голову сложить". В каком-то месте пути попадается развилка, где нужно принимать решения. Около развилки пути еще очень близки, но дальше они ведут витязя к совершенно разным приключениям.
Или можно представить себе балку прямоугольного сечения, на которую положен груз. Кладем сверху гирьки, увеличиваем груз, балка сжимается и остается прямолинейной. Но, начиная с некоторого критического веса, она уже не может оставаться в этом положении и прогибается вправо или влево. Ей приходится "выбирать", куда прогнуться под действием случайных факторов.
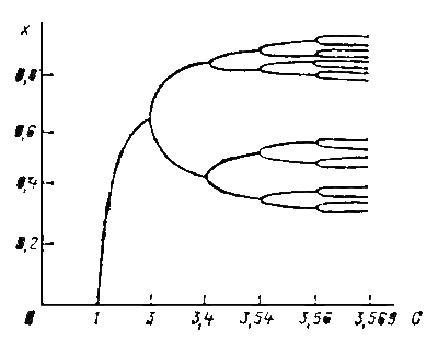
Если нарисовать зависимость максимального прогиба балки от массы груза, то получиться так, как показано на рисунке.
Такие картинки называют бифуркационными диаграммами.
Представим себе какую-либо систему (физическую, химическую или биологическую), зависящую от параметра (от времени, температуры, концентрации, коэффициента воспроизводства или какой-то иной величины). Мы "крутим ручку" под названием "параметр" и состояние системы немного меняется. Немного крутим - немного меняется. Но иногда число возможных состояний системы , соответствующих одному положению ручки, может меняться, а иногда прошлое состояние системы может не слегка измениться, а исчезнуть, и система оказывается вынуждена совершить катастрофический скачок. Эти значения параметра называют точками ветвления или точками бифуркации. Такое поведение отвечает за множество явлений природы - от радуги в небе до опрокидывани буровых платформ на морском шельфе, от гигантских нашествий саранчи до потери управляемости летательных аппаратов…
Замечательным результатом науки XX века стало понимание того, что различных типов бифуркаций очень немного. Сложные системы, как это не удивительно, очень часто претерпевают те же самые скачки, бифуркации, метаморфозы , что и простые.
Оказалось, что движение жидкости в причудливом турбулентном потоке, "коллективные усилия" излучающих атомов, создающих лазерный луч, и изменения популяции насекомых определяются, по существу, одинаковыми законами. Их поведение похоже на оркестр, прекрасно управляемый дирижером. Конечно, дирижер ограничивает возможности каждого из оркестрантов. Зато у целого появляется совершенно новое качество - способность вести себя согласованно, просто, гармонично. Одна из удивительных вещей состоит в том, что во всех этих системах "дирижера" никто не назначает. Он возникает в ходе самоорганизации, отбирающей из океана возможностей ничтожную толику и упорядочивающей поведение системы".
Более детально бифуркационная диаграмма показана на следующем рисунке.
Илья Пригожин. ДЕТЕРМИНИЗМА НЕТ НИ В ОБЩЕСТВЕ, НИ В ПРИРОДЕ (2000)
Cовместный проект российского журнала "Эксперт" и "Лос-Анджелес Таймс Синдикат Интернэшнл". Статья написана лауреатом Нобелевской премии по химии за 1977 год Ильей Пригожиным. В формулировке шведских академиков, Пригожин был отмечен "за вклад в термодинамику необратимых процессов и, в особенности, в теорию диссипативных систем". С не меньшим основанием бельгийского ученого и нашего соотечественника (Пригожин родился в Москве в 1917 году и был вывезен родителями из России в 1921 году) можно было бы наградить и за исследования в области физики, и за вклад в биологию. Фундаментальная проблема, которой занимался и продолжает заниматься Илья Пригожин, не имеет дисциплинарных рамок. Речь идет о так называемой "стреле времени" в естественных науках. Вплоть до второй половины XIX века идеалом для естествознания были законы динамики, симметричные относительно времени (прошлое и будущее для динамической системы абсолютно эквивалентны). Некоторую сумятицу в умы внес открытый более ста лет назад Второй закон термодинамики, утверждающий, грубо говоря, что предоставленная самой себе термодинамическая система будет стремиться от порядка к хаосу, причем процесс этот необратим, или "направлен во времени". Но полноценное включение "стрелы времени" в науки о природе произошло только во второй половине уходящего столетья, и связано это прежде всего с работами Ильи Пригожина, показавшего, что направленность во времени - фундаментальное свойство всех естественных систем (физических, химических, биологических и даже социальных), причем "естественное стремление" к хаосу отнюдь не ведет к утрате гармонии. Пригожину удалось объяснить на языке математики, что хаос может быть конструктивен - он порождает новый порядок.
Историк экономики Фернан Бродель однажды написал: "события приходят и уходят", имея в виду, что история не делает скачков и события не более чем искусственно локализованные наблюдателем элементы в непрерывном потоке времени. Биохимик Федерико Майор, в прошлом возглавлявший ЮНЕСКО, отстаивает другую точку зрения: непрерывность исторического процесса просто скрывает ключевую роль отдельных событий. Прежде чем разобраться, кто из них прав, зададимся вопросом: а что мы, собственно, понимаем под "событиями"?
Жидкость с творческими наклонностями
Наверное, мы согласимся с тем, что и революция 1917 года в России, и падение Берлинской стены были "событиями". И то и другое могло произойти, но могло и не произойти. Тем не менее точное расположение Луны и через тысячу лет вряд ли станет "событием", поскольку его можно рассчитать с помощью законов Ньютона. Событие - это то, что нельзя заранее вычислить, это продукт творчества исторических сил.
Гуманитарные науки в течение долгого времени отвергали детерминистические законы из-за свободы выбора, присущей человеческому обществу. Но может статься, что природные системы также не столь детерминистичны, как нам до недавнего времени пытались навязать физика с биологией.
Естественную историю тоже двигают события. У природы тоже есть своя "свобода выбора", которая проявляется в точке бифуркации (точка "раздвоения" траектории системы, в которой нельзя точно спрогнозировать, какую именно траекторию она выберет в ближайшем будущем. - "Эксперт"), поэтому для сложных природных систем будущее не более предсказуемо, чем для систем исторических. Так как свобода выбора связана с творчеством, можно сказать, что природа в состоянии творить.
Пожалуй, наиболее яркий пример творчества природы - разнообразие биологических видов. В настоящее время, например, науке известно свыше 12 тысяч видов муравьев, и трудно представить, что появление всех этих видов было запрограммировано в момент Большого взрыва.
Впрочем, природное творчество можно наблюдать и на более примитивных уровнях организации материи. Разве не творчество сам Большой взрыв - рождение материи и излучения из квантового вакуума? Или рассмотрим менее масштабное явление - вихри Бенара. Если в тонком слое жидкости довести разницу температур между нижней (подогреваемой) и верхней (при комнатной температуре) поверхностью до определенного уровня, то мы обнаружим появление вихрей, разделяющих объем жидкости на регулярные ячейки. Неупорядоченное на микроскопическом уровне движение частиц жидкости с повышением температуры не становится более хаотичным, а наоборот, самоорганизуется и образует порядок на макроскопическом уровне. Похоже, что Бенаровы вихри не признают классической формулировки Второго закона термодинамики, в которой особо подчеркивается деструктивная роль энтропии и диссипации энергии. Напротив, отдаление от равновесного состояния приводит к новой гармонии: подогреваемые частицы жидкости, "выбирая" новые траектории, проявляют "творческие наклонности".
О роли личности в истории сегодня уже ясно, что природа ближе к биологии и истории человечества, чем к классической физике, поскольку в ней всегда присутствует элемент случайности. Но вернемся к "событиям". Они не изолированные явления, а результат взаимодействия множества факторов. В 1917 году революция и крах самодержавия в России могли принять различные формы. То, что произошло в реальности, стало следствием многих причин, в частности слабости царя, непопулярности царицы, нерешительности Керенского и решительности Ленина. Именно эти "микрофакторы" и амплитуда их флуктуаций и определили исход кризиса.
Современная наука позволяет нам лучше разобраться в механизме событий. Как уже было сказано, в физике и химии "события" - это бифуркации. Если проследить за траекторией системы, может оказаться, что в каких-то ситуациях траектория становится все менее устойчивой и распадается на множество новых траекторий. По какой из этих ветвей пойдет система - предугадать невозможно. Малейшая флуктуация может определить будущее миллиардов частиц, организуя их на надмолекулярном уровне. Так вот, верна и обратная аналогия, человеческую историю можно рассматривать как последовательность бифуркаций, и это не просто естественнонаучная метафора. Как на бифуркацию можно посмотреть, например, на переход из палеолита в неолит, который произошел практически одновременно во всем мире. Это бифуркация, связанная с появлением новых форм систематической эксплуатации растительных ресурсов и земных недр. Но разные системы пошли по разным траекториям, образовалось несколько ветвей, таких как китайский неолит, ближневосточный неолит или доколумбов неолит. При переходе к неолиту появились иерархические общества в результате того, что разделение труда породило неравенство. Это, в свою очередь, привело к появлению рабства, которое существовало вплоть до конца XIX века.
Я убежден, что мы приближаемся сейчас к такой же точке бифуркации, после прохождения которой человечество окажется на одной из нескольких вероятных траекторий. Главный фактор - информационно-технологический бум. Мы подходим к созданию "сетевого общества", в котором люди будут связаны между собой так, как никогда ранее. Хорошо это или плохо? С точки зрения долгосрочной биологической эволюции вопрос можно поставить следующим образом: на что будет больше походить сетевое общество - на большой иерархически организованный муравейник или на общество свободных людей?
С ростом народонаселения планеты повышается вероятность нелинейных микрофлуктуаций, связанных с индивидуальной свободой выбора, поскольку увеличивается численность игроков. С другой стороны, поскольку люди становятся все более объединены сетями, может появиться и обратный эффект: императивы объединенного коллектива подавят индивидуальную свободу выбора. И "муравьиный опыт" здесь вполне уместен. Существует множество видов муравьиных колоний; некоторые из них не так велики и насчитывают несколько сотен отдельных особей, другие же - целые империи с миллионами существ. "Социальное устройство" колоний первого и второго типа существенно различается - в небольших колониях отдельные муравьи ведут себя независимо, самостоятельно отправляются за фуражом и приносят свою добычу в муравейник. В больших колониях все подчинено коллективным движениям и роль индивидуальной деятельности сведена к минимуму. Человеческое общество, связанное единой Сетью, вполне может продолжить свое развитие по второму сценарию. На эту мысль наводит еще одно соображение. Несколько лет тому назад меня заинтересовала теория транспортных потоков. Я установил, что в условиях относительно свободного трафика каждый водитель ведет себя более или менее свободно. Такой режим движения я назвал индивидуальным. По мере нарастания плотности трафика вступают в силу законы "коллективного режима" движения, в котором каждый подталкивает другого и испытывает аналогичное воздействие со стороны - водители становятся более связанными друг с другом, транспортный поток начинает подчиняться законам "большого муравейника".
Конечно, потеря свободы человечеством кажется нам не лучшим выходом из новой бифуркации, правда, и мир, в котором "все решает случай", вряд ли кого устроит. Где лежит компромисс, возможна ли иная траектория? Точного ответа дать не может никто, но, глядя на сегодняшнее человечество с позиций теории неравновесных процессов, вот что можно сказать наверняка: глобализация и сетевая революция ведут не только к большей связанности людей друг с другом, но и к повышению роли отдельного индивида в историческом процессе. Точно так же, как в точке бифуркации поведение одной частицы может сильно изменить конфигурацию системы на макроскопическом уровне, творческая личность, а не безликие восставшие массы будет все сильнее влиять на исторические события на новом этапе эволюции общества.
|